Hakka.Finance 是个致力满足全世界不论种族与地区的投资人需求的 DeFi Ecosystem。《史上最完整 DeFi 固定利率协议大图鑑(上)》于 1 月 10 日首度刊载于 Hakka Finance 官方 Medium 部落格,讲述 9 种固定利率协议,并根据使用的机制对其进行分类。本文由 Hakka Finance 创办人 Ping Chen
、执行长 Lucien Lee 与研究员 Ethan C. 共同撰文并授权转载。
DeFi 的发展日新月异,交易和借贷是最重要的两大支柱。
在交易方面,金融史上前所未有的 AMM 模式胜过了 orderbook,成为链上流动性的典范;而借贷这边也从 p2p lending 全面转向 p2pool 的模式。Aave 的前身 Ethlend 向我们示范了 orderbook 方式的 p2p 借贷模式,虽然有著明确到期日及固定利率的好处,但在没有足够流动性,配对效率极为低下,因此被 DeFi 市场给淘汰。取而代之的是 Compound、Aave 等由供需控制利率的永续资金池借贷模式。
然而,少了到期日,借贷需要靠别的力量来维持供需均衡,在 lending pool 中便是“利用率 – 利率”的回授控制机制:供不应求的时候升息,鼓励存/还款;供过于求的时候降息,鼓励借/提款。儘管 Aave 号称有固定利率借款功能,但其实还是对固定利率借款保有调高利息的机制。可以说利率浮动是永续借贷资金池的必然现象。
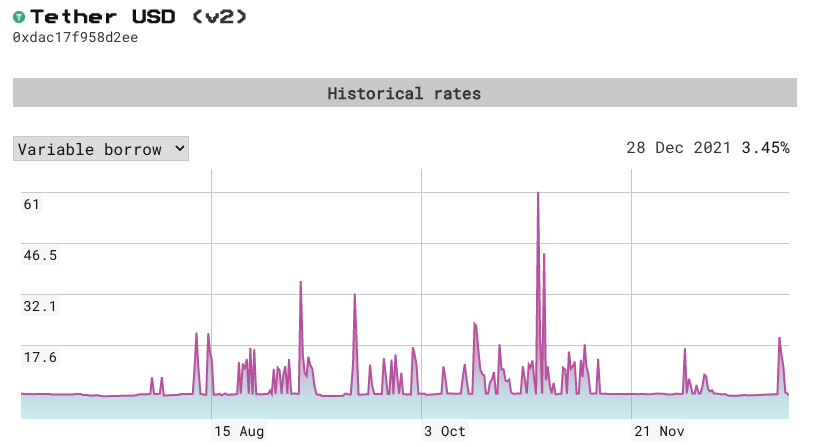
然而浮动利率不利于人们进行长远财务规划与槓杆交易,尤其是 DeFi 中利率的高波动性,使得浮动利率贷款风险极高,以 2021 下半年 Aave 的 USDT 借款利率为例,其利率波动不仅大并且十分剧烈,一天内利率能从 3.73% 瞬间陡升到 61%(2021/10/29~30)。
如此高不确定性阻碍了 DeFi 更大市场规模的发展,反观传统金融大多数债务市场都是由固定利率贷款驱动,稳定可预测利率能让贷款/借款人对他们的投资组合有更多掌控感,进而愿意採用更多複杂的金融商品。
同时借贷做为建构投资组合的基础元件,通常被期待拥有可预测的利率,譬如以固定收益产品,如不动产抵押债券、公共债券为基底,组成的保本型基金,或者以固定利率借款的比特币槓杆仓位。可预测利率可以说是发展现代化金融商品的基石。
撰写本文时, DeFi 借贷协议的未偿债务总额约为 236 亿美元。相比之下,全球债务市场估计为 128 兆美元,随著更多使用者与机构进入 DeFi 市场,固定利率的需求绝对是持续蓬勃增长。因此,我们大胆预测,固定利率协议将成为 DeFi 的新圣杯,也会是下一波 DeFi 爆发成长不可或缺的基础。
DeFi 中的固定利率机制
DeFi 是利率收益资产(Yield)繁星交织辉煌的银河,不论是借贷、AMM LP 交易手续费、流动性挖矿、收益聚合⋯⋯等等,DeFi 四处充斥利率收益资产,而区块链上的利率都是由市场力量动态决定,因此他无时无刻都在浮动。为了因应市场对于不同风险的偏好,因此有许多产品尝试打造固定利率 DeFi 产品,而其中又以固定利率借贷为最大宗,使用者希望存款时能提早掌控未来的收益,或于借款时就确定借款成本,以免因市场波动而使借款成本超出预期。
本文将涵盖 Yield Protocol, Notional Finance, HiFi, Pandle Finance, Element Finance, Swivel, Sense Protocol, Barnbridge, Tranche 等 9 种固定利率协议,各个协议形成固定利率的方式都不同,接著我们将根据使用的机制对它们进行分类。

机制总览
首先,最关键的就是“固定利率”的来源。
前述提到 Compound/Aave deposit 等浮动利率是源自 lending pool 的供需力量起落,若一个人要得到不受市场波动影响的固定收益时,势必得摆脱跟池子交易的模式,找到另一人做为对手,提出支付一定利息的保证。而这样的保证利息来源有两种:一种是由借方支付固定利息,另一种是透过贷方的利息重分配来达成。
1. 固定利率借贷: Fixed-rate Loan
由借方支付固定利息的方式本质上和 Bitfinex 放贷相去不远,都是透过约定日期、约定额度、固定利率的方式进行借贷,只是改用一些比较适合区块链的方式,譬如将 p2p 借贷改为 p2pool,透过 AMM 借贷做价格(利率)发现。
一种实现此目的之机制为“交易零息债券”。零息债券(Zero coupon bond)是不支付利息的债券,但通常他的交易价格会低于面值,到期后会按面值支付给债券持有人。贷方以折价购买零息债券相当于固定利率存款,可于到期日时领取面额上的资金,而借方则可透过抵押资产来借出零息债券并折价卖成现金,想取回抵押品需于到期日后归还零息债券上面额的欠款,从系统借出之零息债券面额和卖出后得到之现金的差即为借款利息。由于借款的成本即为存款的收益,因此可透过市场供需达到均衡,来决定借贷双方都能接受的固定利率。
举例来说,借方抵押资产后发行一张一年期的面额 $1,100 零息债券,然后在市场上以 $1,000 折价卖给贷方。贷方相当得到一年期固定利息 10% 的 $1,000 债权,而到期时借方必须支付票面面额 $1,100 去赎回零息债券,对借方来说,他也得到了一年期固定利息 10% 的 $1,000 借款。用零息债券设计固定利率的好处在于,因为零息债券因为没有利息,所以不像有息债券会面临再投资风险。也就是当你领到利息后,将赚到的利息再重新投资时,因为市场利率随时都在变动,你的总收益也因此不可预期,得承担市场利率变动的风险。可以说零息债券是一个在购买当下,就能完全确定收益的投资工具。
相关协议:Yield Protocol, Notional Finance, HiFi
2. 利息重分配: Yield Redistribution
前者本质上是一个独立的借贷市场,而另一种方式则是基于既有的利息来源,可以是浮动利率的存款,也可以是 Yield Farming,衍生出一个交易利率的次级市场。而根据交易模式不同,又可以再分成本金-利息拆分与结构型商品两种。
2–1. 本金-利息分离(Split Principal & Interest)
给定一个收益来源,我们可以将投资的回报拆分成本金和利息两部分,并分别定价。比方说,你可以将“存进 Aave 的 $10,000 USDC 一年后会赚到的利息”做为一个商品贩售,如果有人愿意出 $400 USDC 买它,那你实际上就得到了一个 4% 的固定收益投资。你也可以理解成 A 和 B 两人分别出 $9,600 和 $400 一起投资到 Aave,并约好一年后 A 拿 $10,000 而 B 拿到剩下的部分,达到事先约定利润分配的效果。实现以上目的之作法为,将借贷协议中的本金和利息拆分,并将两者皆代币化。利息代币在结算前的定价取决于市场对未来利率的预期,而本金代币则相当于零息债券,能于到期日后按面额赎回资产,在到期日前零息债券会根据该资产在市场中的时间价值而产生折价。
从以上的例子,很容易理解本息分离如何做到固定利率贷款,另一方面若要做到固定利率借款,可以透过在借款当下买入利息代币,理论上只要借款与贷款利率之间的波动相关性非常紧密,借款的利息浮动会被贷款的利息代币的价值浮动相消,因此达成固定利率借款的效果。而实际上借/贷款利率走势之间,根据资金使用率的状况,并不一定完全相同,因此只会达成部分对冲效果。
相关协议:Element Finance, Pendle Finance, Swivel, Sense Protocol
2–2. 结构型商品(Structured Product)
在借贷协议中存款利息的大小为浮动的,既然未来利息具不确定性,且每个人有著不同的风险承受能力和资金的机会成本,那就可以将根据个人的需求去重新分摊风险。
结构型基金可针对投资人对市场预期的不同,将利息收益拆分成不同等级,并将其重新组合成不同的金融衍伸品。
它本质上是一种融资槓杆,但因为贩售固定利率债券的收入通常也会被用于增持相同的变动利率资产,所以实际上的效果和本金-利息拆分类似,也是一种利率的再分配。举例来说,我们可以设计一个以 5% 为界的双层架构基金,A类为风险较低但优先收益分配的产品(固定利率),B 类为风险较高但高收益的产品(浮动利率),基金的钱全部都拿去 Aave 裡放贷,若最终累积利息超过 5%,A 类投资人只能拿约定好的 5% 收益,而 B 类投资人可以拿其馀的超额报酬。反之不到 5% 时, B 类投资人的钱会拿去填补 A 类投资人利息不足 5% 的部分,直到 B 类投资人的投资全部赔空。
相关协议:BarnBridge, Tranche
各协议介绍
固定利率借贷
在 DeFi 中实现固定利率借贷最容易的方式是透过铸造/购买零息债券。
零息债券是一种借据,发行商承诺持有人可以在到期日时以 1:1 换回面额价值的资金,但由于资金具时间价值,因此在到期日之前零息债券会折价在市场上流通,折价的大小则由市场利率以及到期时间而异,折价越大代表到期时之收益越高,反之亦然。
贷方以折价购买零息债券,并于到期日时按面额大小赎回资产,相当于以固定利率借款;而零息债券则是由借款方所提供,借方先以超额抵押资产后,再铸造出零息债券并卖成现金,以达成固定利率借款的效果。
各家差异主要在于零息债券如何用适合区块链的方式定价,我们将在后面 AMM 章节深入讨论。

Yield Protocol
Yield Protocol 为使用零息债券(fyDai)作为实现固定利率借贷的协议,在到期日之后 fyDai 能以 1:1 赎回 Dai。
固定利率存款和借款的机制如下:
- 固定利率存款:先以折价购买零息债券 (fyDai) 在于到期日后赎回,收取固定利息。
例如:Alice 以 1000 Dai 购入 1050 fyDai,若一年后到期,届时可换回 1050 Dai,相当于 5% 固定年化存款利率。

- 固定利率借款:先存入 ETH 当抵押品,并铸造出 fyDai 再卖成 Dai,由于 fyDai 会折价,因此拿到的 Dai 数量变少,两者之差额即为预先锁定的借款成本。
例如:Bob 在协议中抵押 1 ETH,以 5% 年化借出 1000 个 Dai,若到期日为一年后,代表 Bob 欠系统 1050 fyDai,需归还欠款后才能赎回抵押物。
值得一提的是,在 Yield Protocol V1 中整个服务搭建于 MakerDAO 上,因此能于到期日之后,将整个借贷的仓位转移至 MakerDAO 内,使固定利率转为浮动利率,此时存款方能收取 Dai Saving Rate,而借款方则需支付 stability fee。
而在新版的 V2 中则捨弃了与 MakerDAO 的连动,但也因此打破了 MakerDAO 的限制,得以支援更多的抵押品,包含 yvUSDC、ENS 等,并能支援其他币种的借款,如 USDC。
此外,由于零息债券的价值会随时间变动,因此 Yield Protocol 创造出了一条新的 AMM 曲线 YieldSpace,该曲线之特殊性质适合作为零息债券的流动池,还能提高资金效率,已成为相关协议之 AMM 标准。
流动性仓位管理
由于每一期的零息债券都有不同的到期日和价格,因此每期皆需有独立的流动池以供人交易。 目前 Yield Protocol 每一期为六个月,为了不让流动性提供者频繁的调仓,流动性会于到期后被自动转至最新的一期,如此一来流动性提供者无需花费 gas fee 即可持续赚取手续费。
Notional
Notional 同样以交易及抵押铸造零息债券 (fCash) 来达成固定利率借款,借贷利率由市场供需来决定。
与 Yield Protocol 最大不同的地方在于,Notional 系统中的底层资产为 cToken,也就是 Compound 的存款凭证,交易零息代币的流动池为 fCash/cToken,使流动池中存放的资金都能随时间产生利息,增加流动性提供者之资金使用效率。
固定利率存款和借款的机制如下:
- 固定利率存款:借款方支付 DAI,系统会先将其存入 Compound 中换得 cDAI,再至流动池中购买零息债券 fDAI,购买的价格即决定了固定借款利率之大小。
- 固定利率借款:抵押 ETH 之后,可铸造出 fDAI,再将其卖成 cDAI,最终至 Compound 取回 DAI 以实现固定利率借款,fDAI 和 DAI 之差为借款成本。
由于池内底层资产为 cToken,因此在到期日后存款之固定利率会自动转变成 Compound 的浮动利率。
流动性统一管理
在 Notional 中的底层资产为 cToken,虽然协议中同时会有很多期的零息债券,但想做为流动提供者仅需于于统一的入口存入 cToken,系统会将集中的流动性自动分配至各个池内,实际分配的比例则由社群治理来决定。

存入 cToken 后会拿到 nToken 作为流动性凭证,该凭证无到期日,且可赚得利息和交易手续费,甚至还能做为 Notional 中的抵押品,从协议中借出资产。
HiFi
HiFi Finance 前身为 Mainframe ,是一样利用零息债券的固定利率借贷协议,原理上与 Yield 并无二致。都是透过借方抵押资产,借出零息债券,卖给贷方来达成固定利率的效果。
在他们 v0 版的白皮书中,比较特别的地方在于,留有清算担保池能直接为清算抵押率不足的债务(类似于 liquity 的机制),另外清算担保池与借款抵押品,也能用于闪电贷(flash loan)赚取收益,让閒置资金获得更多利用。

然而,目前 HiFi v1 的设计上,已经跟 Yield 毫无差异。不仅 AMM 模型基于 YieldSpace,同时清算担保池的设计也不见踪影。取而代之的是,提供脚本工具让清算者使用 Uniswap v2 闪电换(Flash swaps)清算债务,而这也与其他产品十分类似。
利息重分配
如前章所述,将借款凭证作为零息债券,再以折价卖给存款方即可实现固定利率借贷,此时利息的来源为借贷双方于市场中搓合之结果。
而另种实现固定利率的做法为,将系统内所有资金都先存入借贷协议或是收益聚合器领取浮动利率,再根据每个人的风险偏好去重新分配利息。
此种重新分配贷方利息的做法,又可分成“本金-利息代币分离”以及“结构型商品”二类,各相关协议之介绍如下:
本金 — 利息分离
将资金存入借贷协议或收益聚合器中之后,我们可把存入的本金和未来的利息拆分,并将其代币化。
本金代币可于到期日后按 1:1 赎回底层资产,虽然在此模式中无借款行为,但其性质仍可等效于零息债券;而利息代币代表的则是未来会产出的利息,兑现未来利息之机制因协议而异。
各家差异主要在于本金代币和利息代币如何用适合区块链的方式定价,我们将在后面 AMM 章节深入讨论。
其中利息代币又分为以下两种模式
- Drag — 已实现利息会累积到期时才能领取(Past yield delivered at maturity)
- Collect — 已实现利息不断转移给持有者(Past yield delivered before maturity)
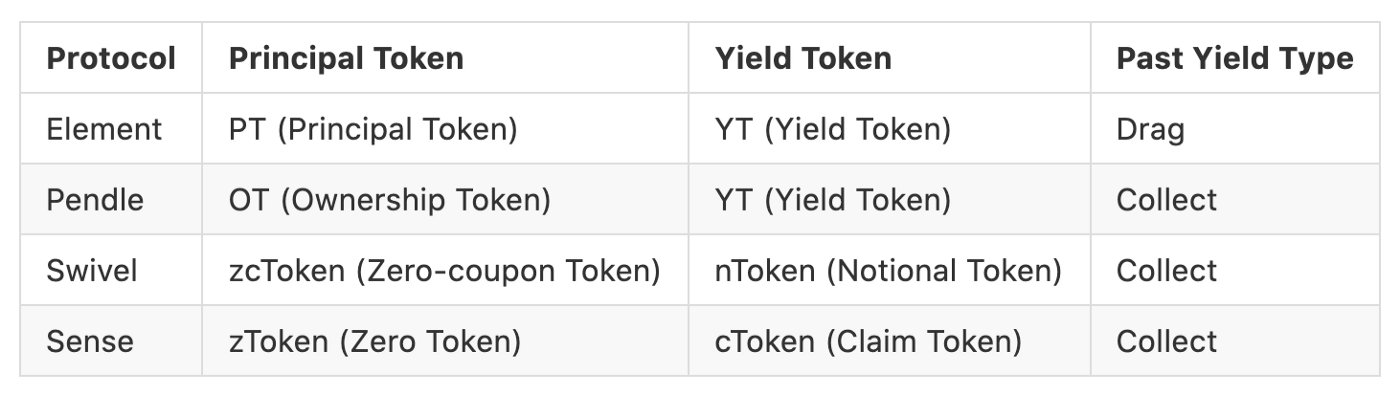
Element
在 Element 中所有的资金会存入 Yearn Finance 内,并将存入的资金拆分成本金代币 (PT, Principal Token) 和利息代币 (YT, Yield Token)。
本金代币相当于零息债券,可于到期日后将本金部位赎回;而利息代币则代表未来利息,可于到期日后兑换出期间实际产生之利息。

在此系统下,我们可以创造出“固定利率存款”和“槓杆做多利率”的市场
- 固定利率存款
购买本金代币相当于以固定利率存款,而年化的大小由本金代币的价格来决定,价格越小代表到期时的获利越多,年化利率越高,反之亦然。

另一种作法为在 Element 中存入资金后,直接将铸造出来的 YT 卖掉,提早变现未来利息以实现固定利率收益。
- 槓杆作多未来利率
利息代币 (YT) 的价格代表市场对未来利息的预期,而期间累积利息越高 YT 的结算价就越高。
我们能透过购买 YT 来槓杆做多利率,只要于到期日后能赎回的资产高于购买成本,即可从中获利。

除了直接购买 YT 外,另一种作法为先于 Element 中存入资金,并将 PT 卖出,再将所得之现金重複存入 Element 内,反覆执行,以最大化手中 YT 数量。
Pendle
Pendle Finance 与 Element Finance 类似,也会将存入的资金拆分成本金代币(OT, Ownership Token)和利息代币(YT, Yield Token),主要的不同在于利息代币运作机制。

在 Element 中,本金产生的存款利息会累积于利息代币内,累积的利息越多,结算后的赎回价就越高;而 Pendle 中本金产生的存款利息则会直接发放给利息代币的持有人,持有利息代币代表能拥有到期日前持续获得利息收益的权利,而随著到期日的接近,这个权利的时间价值会递减,最终归零。
- 固定利率存款
若想在 Pendle 上实现固定利率存款,须先将资金存入协议中,铸造出 OT 和 YT 后再将 YT 卖掉,提前套现未来利息,赚取固定之存款收益。
- 槓杆作多未来利率
同样的,对于看涨利率的投资人来说,也能透过购买 YT 来槓杆做多利率,只要 YT 的购买成本低于其产生出的利息即可从中获利;或能透过存入资金,并将 OT 卖出,再把所得现金重新存入 Pendle 内,反覆执行前述步骤以最大化手中 YT 数量,加大做多利率之槓杆。
- 固定利率 AMM LP 交易手续费
除了借贷协议与收益聚合器之外,Pendle 还支援以 Sushi LP token 作为底层资产,将未来因交易手续费而产生的收益代币化,也同样能以固定利率存款或槓杆做多未来利率。
Swivel
Swivel 前身为 DefiHedge,其原理一样是将资金放入收益协议后,把资金拆分为本金(zcTokens) 与利息(nTokens)两种代币,透过在期初卖掉利息代币,并保留本金代币来获得固定利率,而另一方利息代币的持有者则得到浮动利率。存款利息与 Pendle 类似,会持续发放给利息代币的持有者。

Swivel 与其他本息分离的协议最不一样的特色在于,其他人都试著使用 AMM 来提供本金代币与利息代币的流动性,但他选择了链下订单簿来作为交易模型,其原因我们将在 AMM 章节深入讨论。
Sense Protocol
Sense 延续一样的模式,将资金拆分为本金代币(Zeros)和 利息代币(Claims),存款利息与 Pendle 类似,也会持续发放给利息代币的持有者,但交易机制略有不同,我们将在 AMM Curve 章节进行更多比较。
结构型商品
分级基金(structured fund)又称为结构化基金,他是通过对基金收益或是淨资产的分割与再分配,打造出不同等级风险收益不同的投资标的。常见情况是分为两级,一级收取固定报酬,另一级则收取剩馀报酬。
假设我们称“预期风险和收益均较低且优先享受收益分配的部分”为“A 类份额”,另一类“预期风险和收益均较高但次后分配收益”的部分称之为“B 类份额”,B 类份额本质是“借用”A类份额的资金来放大收益,而具备一定槓杆特性,也正是因为“借用”了资金,B 类份额具支付 A 类份额约定利息的义务。
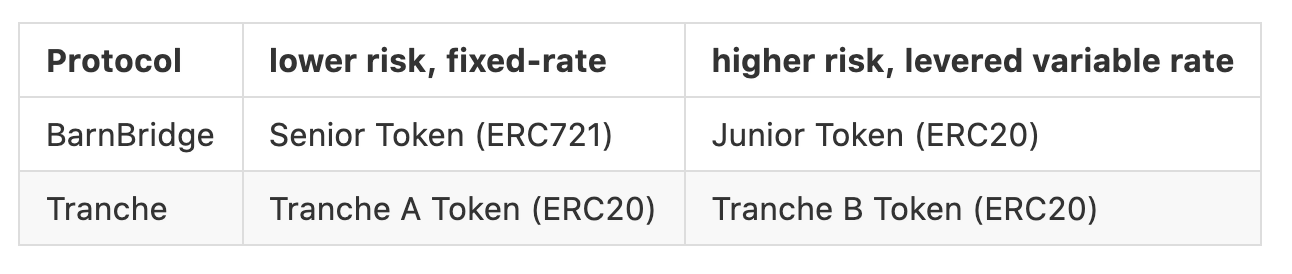
BarnBridge
BarnBridge 是利率结构型商品,由 Junior Pool 和 Senior Bond 组成。两者的资金都会被投入到底层的协议(Compound, Aave)去产生利息,但收益分配的方式不同。
Junior Pool 的流动性提供者会拿到 ERC20 token,代表他的投资份额。Junior 没有到期日,并且领取变动收益。而购买 Senior Bond 的人能自选投资时间(最长一年),仓位会以 ERC721 的形式持有,Senior 可以得到固定收益,但在到期日之前不能提早赎回,只能转让 NFT。

由于底层协议的利率是浮动的,有可能会忽然变很低。为了确保 Senior Bond 的持有者都能在到期时兑回承诺的本金和利息,Junior Pool 的部分流动性会被锁定。因此,Junior 的赎回要经过特定的流程,有两个选择:
- 立即赎回:预先扣除承诺要分给 Senior 的部分,剩下才能领回
- 换成债券延后赎回:根据 Senior 的加权到期日 mint 出 NFT,到期日后才能赎回,不额外扣除费用
至于 Senior Bond 的利率则是透过以下公式决定:

其中 yield rate 是取 Compound/Aave 利率的三日平均值,再根据池内的流动性利用率打折,成为 Senior Yield。因为 Senior Yield 总是 <= 底层协议当下的利率,所以长期而言 Junior 可以赚取额外报酬,但是在利率忽然暴跌的时候可能出现少赚,甚至赔钱的情形。
Tranche
Tranche Finance 和 BarnBridge 类似,都是结构型产品,分成固定利率的 Tranche A 和浮动利率的 Tranche B(两个都是 ERC20 token)。
但不像 Barnbridge 会根据池中固定/浮动的比例决定利率,Tranche 完全没有自动化的利率决定机制,取而代之的是由 DAO(token holder)透过投票的方式“决定”要发给“固定”利率的人多少利息。所以本质上 Tranche A 并不是真的固定利率,随时可能被投票改高或是改低利息。

可以看到 FIXED 和 VARIABLE 的利差很大,而且 governance 可以片面决定 FIXED 要改多少。
零息债券与本息代币专用的 AMM
无论是零息债券、本金代币或利息代币,想要能在市场上被交易就会需要流动性。中心化交易所以是订单撮合 (order matching)的方式让买卖双方成交,流动性是由买卖双方挂单提供,此做法虽然可以让价格发现的过程很有效率,但却不适用于区块链这种计算及储存资源相对稀缺、效能较低的系统。因此在区块链中,发展出了最适合 DeFi 世界的自动化做市商(Automatic Market Maker, AMM),AMM 的流动性会由买卖以外的第三方 — 流动性提供者 — 来提供,报价则由事前所规定好的数学关係式来决定。
不同的数学式会对应到不同的曲线,我们可以根据交易币种的不同,设计出能给予合理报价的关係式。
以 Uniswap v2 为例,採用之恆定乘积做市商模型如下:
x ∗ y = k
此曲线提供的边际报价为 price = y/x,为池内两个币种之存货比,当有交易发生而使存货数量改变,价格就会随之变化,此种模型适合价格波动较大的币种。
另个极端的例子为 mStable,採用之恆定总和做市商模型如下:
x + y = k
此曲线提供之报价恆为 price = 1,无论池内两币种存货如何改变,兑换比永远为 1,适合货币价值完全相同之稳定币互换。
然而,对于零息债券、本金代币或利息代币来说(本金代币本质上是零息债券),他们有个共同的特性是“价值随时间变化”,而以上两种单纯的 AMM 都没有办法很好反应这个特性。接下来我们将讨论针对零息债券与利息代币要如何设计好的 AMM 模型。
零息债券的定价和性质
零息债券的价格可由利率大小和到期时间来决定,公式如下:
零息债券的价格是以面额折价计算,也就是考量到未来现金流複利,折现到现在的价值为多少,公式如下:
债券价格 (PV) = 面额 (FV) ÷ (1 + r)^n
面额:债券的票面价值,到期后能拿到的金额
r:年利率
n:期数(年)
由以上定价公式可知,儘管市场利率不变,零息债券的价格仍会随时间变化,越接近到期日,债券的价格就越接近面额大小,最终两者之兑换率会收敛至 1。
从另个角度来看,若零息债券债券的价格维持不变,随著到期日的接近,年利率 r 就会持续上升。
零息债券适合怎样的 AMM 曲线?
若以 Uniswap 的 x ∗ y = k 作为 AMM 曲线,假若无人交易,池内状态不变,零息债券的价格也会维持不变,则随著到期日的接近 APY 就会不断增加,而吸引人前来套利,使流动性提供者的承受损失;若使用 mStable 的 x + y = k,则零息债券的价格永远都为 1,无法在到期日之前折价交易,表现出时间价值。
由上可知,我们需要一条会随时间演化而自动改变报价的曲线,让零息债券的价格在一开始时对价格变化较敏感,能根据市场状况改变,而越接近到期日兑换率会逐渐收敛至 1。
Yield Protocol 和 Notional 都是以购买或铸造零息债券代币来达到固定利率借贷的协议;Element, Pendle 与 Sense 则是将资产拆分成本金代币和利息代币,本金代币本身也可以视为一种零息债券。以下简介和分析前述五个协议使用之 AMM 曲线,最后讨论不使用 AMM 而採用订单簿的 Swivel。
YieldSpace
Yield Protocol 为了零息债券设计出了一条特制曲线 YieldSpace,该曲线之参数包含时间 t,t 越大代表距离到期日越远,而随著到期日的接近,t 会逐渐趋于零。

可由简单的微积分证明此曲线于 t = 1 时会等价于 x ∗ y = k,而当 t = 0 时,曲线会演化成直线,变成 x + y = k。这让使用者能于到期日之前,根据市场利率来交易债券,且当时间接近到期日,价格会自动接近 $1,最终可以 1:1 赎回债券面额资产,符合零息债券特性。
除此之外,YieldSpace 的曲线还有一个重要的性质为“利率恆定”,儘管代币价格会随著时间而自动改变,但只要没有人来交易,池内两个币种的存量不变,利率的大小就会维持恆定。
因此只要市场利率不变,都不会因时间造成的价格变化而产生套利空间,流动性提供者就不会有 time-dependent impermanent loss。
举例来说,假设今有一档一年期的零息债券,利率为 10%
初始价格为 $0.909 1 ÷ (1.1)^1 = 0.909
半年后价格为 $0.953 1 ÷ (1.1)^0.5 = 0.953
一年后价格为 $1 1 ÷ (1.1)^0 = 1
若都无人交易,代表池内两币种之存量(x,y)不变,并且市场利率维持 10%,六个月后,随著 t 值变小,斜率相对改变,该零息债券的价格会上升至 $0.953;九个月后价格会再提升至 $0.976;最后到 $1。
动态手续费
现今主流的 AMM 都是以“交易量”之固定百分比做为手续费,如 Uniswap V2 手续费为 0.3%,而此机制不适用于零息债券的流动池,因为在到期日之前,0.3% 的手续费会对年化造成巨大的影响。
假设有一档零息债券 APY 固定为 10%,则在不同时间以 0.3% 交易手续费交易,对年化利率之影响如下:

时间越接近到期日,手续费对年化利率的影响就越剧烈,该变化的大小会呈指数递增。

因此在 YieldSpace 中,手续费的计算改由“利息”中的固定百分比来收取,随著到期日的接近,能产生的利息变少,交易手续费也会随之降低。
虚拟流动性:增加资金效率
在正常的情况下,零息债券的价值永远不该高于面额,也就是代币的兑换率永远不会超过 $1,一旦超过即会创造出套利空间。
但在上述的 AMM 设计中,流动性的分佈会对称于 $1,但由于零息债券的价格不会超过 $1,代表流动池内有一半的资金永远是閒置的,不会被交易到,因此 YieldSpace 引入了虚拟流动性,流动池内约一半的零息债券由虚拟存量(virtual reserve)提供,透过虚拟存量来让此曲线能在不影响前述性质的情况下,大幅增大资金使用效率。

灰色区域为虚拟流动性,当 fyDAI 价格高于 1 DAI,系统不允许交易
Notional
由 YieldSpace 的讨论中可了解到,作为一条适合零息债券流动池使用的 AMM 曲线需具备以下三个条件:
- 在利率不变的情况下,能根据到期日的接近自动调整价格以维持 APY
- 随著到期日的接近,价格曲线需越来越平缓,使存量的变化对价格反应不敏感。
- 手续费不能以固定百分比收取,需随著到期日的接近降低
Notional 针对以上三个需求分别引入了以下三个参数:
Anchor
此参数控制价格曲线的中心,其兑换率(fCash per Currency)会随著时间而减小,最终收敛至 1。

若不考虑交易造成的价格滑动,Anchor 的调整能使利率维持恆定,不让时间的变化影响利率的大小。
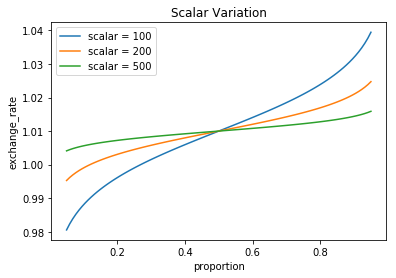
Scalar
此参数代表价格对需求的敏感度,scalar 越小曲线越陡,价格变动越大。 随著时间越接近到期日,曲线会越平滑,使流动性集中于 anchor 所锚定的价格中心。
Trading Fee
手续费的大小会随著时间线性递减至零,以降低手续费对年化利息的影响

Notional AMM Curve
综合以上三个参数可以得到 Notional AMM 的定价公式:

Element Finance
在 Element Finance 中,使用者存入的资金会被拆分成本金代币和利息代币,两种代币有不一样的性质,因而会需要不同的流动池。
本金代币池:
本金代币为能在到期日后将本金赎回的凭证,相当于是零息债券,因此 Element 的本金代币的流动池选择使用 YieldSpace AMM 曲线。
利息代币池:
利息代币可在到期日时赎回期间内所累积的利息,但由于未来利息是不确定的,可能会因市场供需的变化而产生较大的价格变动,因此利息代币的流动池选用 x ∗ y = k 作为较容易做价格发现的曲线。
Pendle Finance
Pendle Finance 同样为本金-利息拆分的模式,与 Element 的差异在于其利息代币的运作模式,持有 Pendle 的 YT 代表领取存款利息的权利,持有越久可获得越多收益,其价值会随时间递减至零。
本金代币池:
Pendle 中的本金代币性质也相当于是种零息债券,但却没採用 YieldSpace 或 Notional AMM 这类适合零息债券使用之 AMM,而是选了 SushiSwap 作为流动池。
SushiSwap 使用恆定乘积做市商作为模型,该曲线不会随著时间而变动,代表流动性提供者会随著时间变化必然会产生暂时性损失。而採用 SushiSwap 作为流动池也就意味著 Pendle 放弃“以 OT 作为零息债券来使用”之性质,让固定利率存款的过程变更複杂,使用者体验变差,可谓相当可惜。
利息代币池:
Pendle 中 YT 在到期时价值必然归零,若以 x×y=kx×y=k 做为 AMM 曲线,则随著时间的流逝,利息代币的时间价值递减,会吸引套利者前来套利,而造成流动性提供者的损失,最终使整个流动池的价值归零。
为解决上述问题,Pendle 参考了 Balancer 的曲线,并多引入了时间相关之参数,使两个币种的权重会随时间而改变。

αi+1: x 于时间 t = i + 1 之权重
βi+1: y 于时间 t = i + 1 之权重
xi 和 yi 为时间 t = i 时流动池内之存量
α 和 β 皆为时间的函数,会随时间变化。
在初始 t=0 时 α 和 β 皆为 0.5
随著时间接近到期日
α 的大小逐渐变小,最终为 0
β 则会逐渐变大,最终为 1。

以利息代币 YT/USDC 池为例,在开始时两个币种之权重比为 50/50,此时 YT 的价格为 $1,随著到期日的接近,YT 的权重会逐渐下降,当权重比下降至 20/80 时,若这段时间无人来交易,则 YT 的价会变为 $1 * (20/80) = $0.25,而最终比例会变为 0/100,此时的 YT 价格即为 $0。
由以上说明可知,此 AMM 曲线能动态的调整报价,符合代币价值随时间递减之性质,以避免流动性提供者承受 time-depedent impermanent loss。

Sense Protocol
Sense 作为另个本金-利息分离型的固定利率协议,其本金代币(zcToken)之性质也相当于是零息债券,而其流动池採用 Sense Space AMM,为前述之 YieldSpace AMM 的改良版。
本金代币:Sense Space
Sense Space 使用了 YieldSpace 之恆等式,但将其中的标的资产(underlying asset)更换成利率收益资产(yield-bearing asset),让流动池内的每种资产都能随时间产生价值,最大化资金效率。
但由于 YieldSpace 的 AMM 曲线会将流动性集中至 1:1 附近,以 zcDAI/DAI 池为例,若只将 DAI 改成 cDAI 作为零息债券的配对资产,则 AMM 无法如期运作。为了解决此问题,Sense Space 多引入了 scaling factor,此参数为 Compound 中 cDAI 对 DAI 的兑换比。如此一来,无论是交易或增加、移除流动性,只要先透过该参数将 cDAI 的价值对应回 DAI 的数量后,就能以 YieldSpace 的公式计算兑换率。
实作方面,合约会于初始化时记录下 cDAI 与 DAI 的兑换率,并于每次交易时更新此参数,如此还能确保 cDAI 利息的累积不会影响零息债券(zcDAI)的美元兑换价值。
利息代币:
Sense 的利息代币设计採用 Pendle 的模式 (Collect YT),但只提供 PT/Target 交易对(Target 在 Sence 中意指利率收益资产)而没提供 YT 流动池。
如果要交易 YT 则需要利用 Target = PT + YT 的关係来兑换。举例来说,在 Sence 上,如果想要购买 Compound Dai 的利息代币(YT):
- 存入 cDai 得到本金代币 zcDai + 利息代币 ccDAI
- 将 zcDai 交易换成 cDai
- 此时手上会剩下 zcDai 跟剩馀的 cDai,可以重複步骤 1~2 ,尽量把 cDai 都换成 zcDai
反过来,若你要卖掉利息代币:
- 跟 Pool 闪电贷出 cDai
- 把 cDai 换成本金代币 zcDai
- 把手上的利息代币 ccDAI 与借来的 本金代币 zcDai 合成赎回 cDai
- 把闪电贷借出的 cDai 还回去
- 手上会剩下一部分 cDai

要成为流动性提供者,也是用类似的方式入池,可以看见以上的方法好处是,我们只需要有一个 本金代币 — 利率收益资产 AMM 池,不需要设计利息代币的交易模型,因此原本两池的流动性能聚合在同一池,进而提高 LP 从交易量而赚得的收益,但很明显的代价是交易的运算过程变複杂了,不仅难以将手上的利率收益资产毫无剩馀地购买利息代币,同时也要付出更多 gas 。
另闢蹊径的 Swivel
最后,身为唯一一个不使用 AMM 定价的协议 ,Swivel 选择以链下订单簿的机制来解决本金与利息代币在 AMM 上定价困难。
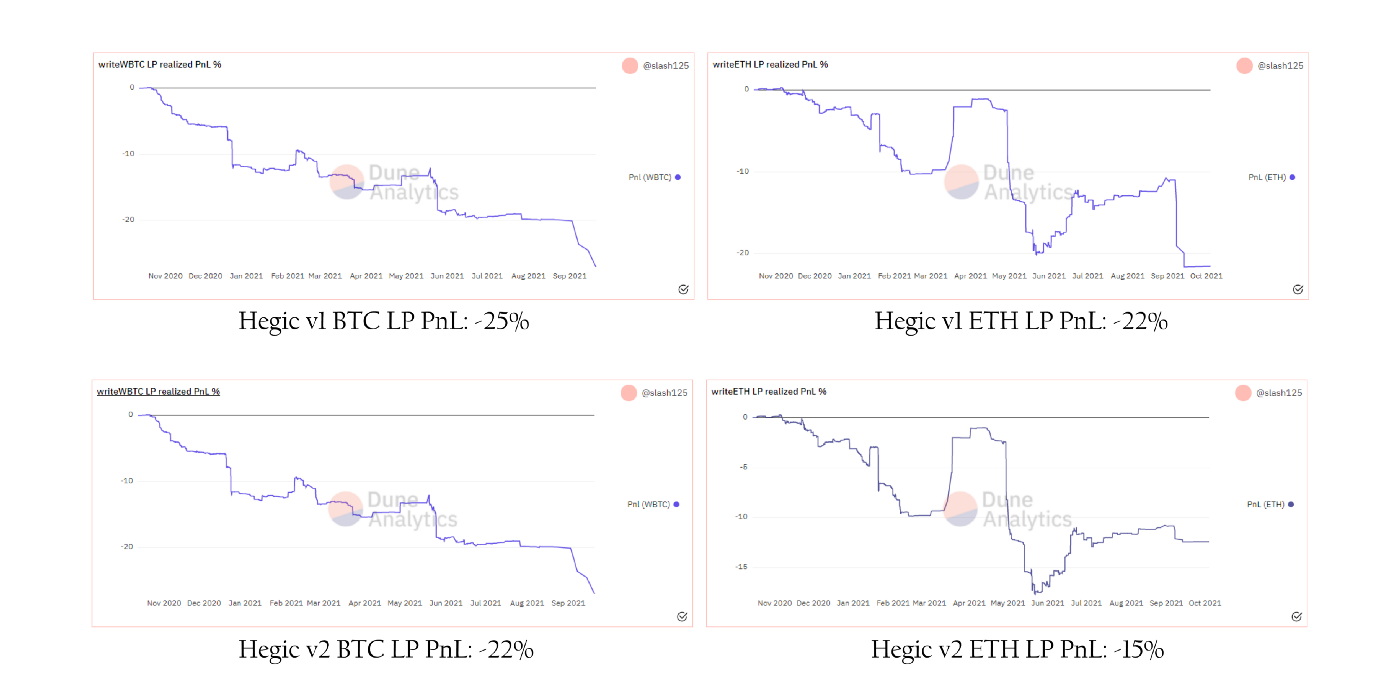
Swivel 认为利息代币等作为利率的衍生品,其价值会随著利率和利率波动的变化,但 AMM 中的利息代币价格难以立刻反应变化。相同的现象也存在于现货市场与其衍生品之间,在选择权市场中,选择权价格不断对现货价格和现货波动做出反应,若要用 AMM 实现 DeFi 选择权市场,其 AMM 模型也必须以某种方式适应这些因素改变。选择权 AMM 虽然发展迅速,但仍难以考虑即时波动性,这导致流动性提供者 (LP) 的回报极低,在 Swivel 对 DeFi 选择权协议 Hegic 的流动性提供者分析中,能发现他们承受了巨大的损失。
因此 Swivel 认为订单簿比起 AMM 适合做衍生品的 DeFi 交易模型,不仅能让 Market Maker 避免定价失真所带来的损失,同时为使用户提供最优惠的价格和最低的交易成本。
除此之外,还可以提供本金代币-利息代币的订单簿交易对,让使用者能直接交换两者,不需要像 Element 一样得在两个 AMM 上做交易(YT-Underlying & PT-Underlying),增加了交易的效率。
资金效率问题和市场效率问题
各个协议实作固定利率的方式略有不同,也因此在“资金效率”和“市场效率”上各有优点和缺点。
固定利率借贷 v.s. 收益重分配
Yield/Notional 的零息债券和 Element/Pendle 的本金代币的性质非常接近,机制却大不相同。
Element 最大的缺点是价格发现的效率非常糟糕,它需要为本金代币和利息代币分别建立流动池,需要更多资金提供流动性。另外,想得到本金代币有两种路径,一个是用现金铸造出 PT + YT 再卖掉 YT,另一个是直接现金买 PT。理论上,在足够有效率的市场,两种路径的产出应该要是完全一样的,但区块链的限制加上 AMM 的特性却会让两者很容易有差额,显得很没效率。
相较于 Element 有两种路径交易本金代币,因此有利差套利问题, Yield 直接了当,只有零息债券交易池,由借贷双方对折现(利息)供需共识来决定价格。但可惜有一好就没两好,Yield、Notional 等固定利率借款方法本质上是一个独立的“初级”借贷市场,不像 Element、Pendle 等本息分离协议,是架构在现有借贷协议上的利率“次级”市场。
固定利率借贷类型协议中,利率的市场均衡是仰赖自身流动池的供需比例来决定,而非已经有大量流动性的底层利率协议。
同时作为一个新兴的借贷市场,得自己重新聚笼资金来创造流动性,相对来说供给/需求弹性会明显较差,若出现供需严重失衡的现象,例如大量存款进入 Yield 购买零息债券,让 Yield 的利率相对于外部利率市场 Compound/Aave 大幅降低时,会需要更久的时间才能达到新平衡。
提升市场效率
值得一提的是 Notional 和 Swivel 对提升效率的尝试。
Notional 的流动性提供者不需要“分配”资金到不同到期日的池子,而是进到一个大池,再由治理的方式统一调度。这件事乍听之下有点危险,但因为 YieldSpace 的特性,现金买零息债券不可能赔钱,顶多只是赚到远低于市场行情的利息,损失时间价值而已。
Swivel 则是直接捨弃 AMM 改用 orderbook,论述大致上也算合理,利率市场和选择权市场类似,複杂到不适合用 AMM 的形式处理。但这裡有个关键点是利率市场的 PnL 不高,所以对交易成本格外敏感,如果 Swivel 因为链下订单簿的限制造成取消/更新 order 的成本很高,恐怕会抵销它高资本效率的优势。
提升资金效率
另一方面,做零息债券的 LP 可能存在著某种本质上的矛盾,因为会想持有这类资产的人理论上就是想赚利息,但流动池中必须有一些现金是没在生利息的。甚至 YieldSpace 为了效率砍掉了一半用不到的流动性,正好就是零息债券的那部分,让池子的平均利率又更低了。所以对 LP 而言,除非交易手续费超过零息债券的利率,否则没有理由把钱分配在 AMM 而不是买债券。
因此 Sense 提出用利率收益资产来与零息债券配对做 LP,让流动池的现金以生息资产的形式存放,但其代价为是使用者进出时,需要多做一层转换增加 gas 的开销。
结构型商品 BarnBridge 的固定利率 NFT 发行并不仰赖 AMM,而是直接在系统内部完成价格发现,最大的好处就是生态中的所有角色的所有资金都处在生利息的状态,没有一丝一毫閒置资金,不过这也不是全无代价的。
从市场构成的角度来看,“固定利率借贷”和“本金-利息分离”是利率的 long-short market,结构型利率协议则是利率的 hedge-speculate market。前者才是比较自然的供需关係,后者的 speculate part 并不是正常的需求,他是为了满足一方想 hedge 而让另一方 take risk 而生。做为对冲风险服务的提供者,对冲风险方的交易对手会希望收到超额报酬,所以长期而言 BarnBridge sBOND 的利率很可能会低于 Yield/Element 的零息债券的利率。
下一步:利率衍生品
在前面的分析中我们反覆强调效率的重要性,是因为利率市场对交易成本非常敏感。对于一年可以 +100% 的比特币来说,0.6% 的交易摩擦似乎不算什麽,但对于 4% APR 的零息债券而言,那是高达获利的 15% 成本!
但话说回来,我们希望从浮动利率过渡到固定利率的真正目的是为了对利率波动避险(或投机)。进一步来说,我们关心的是借/存钱一段时间的实际利率是否和当初预期的相同。真正需要被交易的既不是本金、也不是利息,而是“利差”。
上面介绍到的几个协议产生固定利率的方式略有不同,但都可以视为是利率的现货市场,直观,但效率低下。在利率衍生品市场,我们只需要一点点保证金就可以交易同样名义金额资产的利率。少了本金,对交易摩擦的容忍就变高了,也不需要锁仓大量资本在 AMM 来提供流动性,效率高非常多。
下一章,我们将详细分析利率衍生品的优点,并介绍 Hakka Finance 推出的 iGain — Interest Rate Synth,一款基于利率交换的金融衍生工具。





